Articles
Avertissement
Les articles publiés sur ce site sont destinés à des fins pédagogiques. Toute utilisation commerciale, reproduction ou diffusion sans autorisation est interdite. Bien que nous nous efforçons de garantir l’exactitude des informations, nous ne pouvons être tenus responsables de toute erreur ou omission. Merci de vérifier les informations avant de les utiliser.
Les dB
Pourquoi utilise-t-on les dB en CEM ?
La raison est simple : nous manipulons des grandeurs qui s’étendent sur des plages extrêmement larges. Par exemple, l’intensité électrique peut varier du nanoampère (10⁻⁹ A) au kiloampère (10³ A), soit un facteur de 10¹². Une représentation graphique linéaire de telles valeurs ne permettrait pas de visualiser correctement cette plage : sur une échelle en ampères, la différence entre 1 nA et 1 mA serait invisible, alors qu’il existe pourtant un rapport d’un million entre ces deux grandeurs. L’échelle logarithmique (dB) rend cette variation perceptible en ramenant les rapports multiplicatifs à des différences additives.
Pour les amplitudes
On définit :
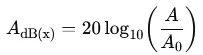
où A0 est la valeur de référence choisie dans l’unité x.
Ainsi, l’unité implicite du décibel est directement liée à celle de A0. Par exemple, si l’on exprime une tension en dBµV, alors la référence est A0=1 μV.
Exemple :
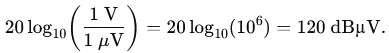
Si l’on choisit une référence différente, par exemple A0=1 mV alors :

On a donc :
1 V =120 dBµV = 60 dBmV.
C’est toujours la même grandeur physique, simplement exprimée avec des références différentes.
L’opération inverse s’écrit :
Ce qui permet de retrouver la valeur dans l’unité choisie (μV, mV, V, etc.).
Pour les puissances
On définit :
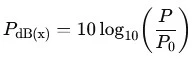
où P0 est la puissance de référence choisie.
L’unité implicite du décibel dépend donc directement de cette référence :
- Si l’on exprime en dBm, la référence est P0 =1 mW.
- Si l’on exprime en dBW, la référence est P0=1 W.
Exemple :
Pour P=1 W en dBm :

Pour la même puissance exprimée en dBW
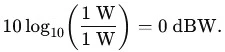
On a donc :
1 W=30 dBm=0 dBW
C’est toujours la même puissance physique, mais exprimée avec des références différentes.
L’opération inverse s’écrit :
Ce qui permet de retrouver la valeur absolue dans l’unité de la référence choisie.
Pourquoi 10 log en puissance et 20 log en amplitude ?
La raison fondamentale est très simple : la puissance est proportionnelle au carré de l’amplitude. Donc prendre un logarithme sur la puissance donne un facteur 10, tandis que prendre le logarithme sur l’amplitude (qui s’apparente à la racine carrée de la puissance) introduit un facteur 20.
Démonstration :
P=V2/R définissons k=1/R et V une amplitude alors P=kA2 et Pref=kA2ref
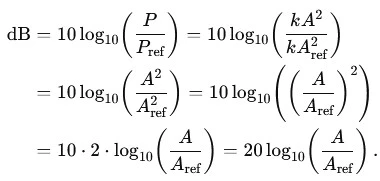
C’est pour cela qu’on écrit 20·log pour des rapports d’amplitude et 10·log pour des rapports de puissance.
Tableau de conversion dB ↔ Facteur
| Rapport d’amplitude | Niveau (dB) | Rapport de puissance |
|---|---|---|
| 0,10 | -20 dB | 0,01 |
| 0,316 | -10 dB | 0,10 |
| 0,50 | -6 dB | 0,25 |
| 0,71 (≈1/√2) | -3 dB | 0,50 |
| 1,00 | 0 dB | 1,00 |
| 1,12 | +1 dB | 1,26 |
| 1,41 (≈√2) | +3 dB | 2,00 |
| 2,00 | +6 dB | 4,00 |
| 3,16 | +10 dB | 10,0 |
| 10,0 | +20 dB | 100 |
| 1000 | +60 dB | 1 000 000 |
Pour convertir rapidement les dB, seules quelques valeurs sont utiles à retenir : 3, 6, 10 et 20 dB pour les autres valeurs, il suffit d’utiliser la propriété des logarithmes.
Propriétés utiles des logarithmes en dB
- log(A⋅B)=log(A)+log(B)
→ en dB, les produits deviennent des sommes.
- log (A/B)=log(A)−log(B)
→ en dB, les divisions deviennent des différences.
Exemple 1 : conversion d’impédance
Prenons 50 Ω exprimés en dBΩ :
- En linéaire, on peut écrire 50 ≈ (10 × 10) / 2.
- En logarithme : 20 + 20 − 6 = 34.
Donc 50 Ω = 34 dBΩ.
Exemple 2 : conversion de champ électrique
Quel champ correspond à 30 dBµV/m ?
- 30 dB = 20 + 10 en logarithme.
- En linéaire, cela donne 10 × 3,16 = 31,6 µV/m.
Donc 30 dBµV/m = 31,6 µV/m.
Attention !
En CEM donner des valeurs avec trop de décimales n’a aucun sens.
- Les tolérances des composants influencent fortement les résultats.
Exemple : un condensateur chimique avec une tolérance de ±20 % induit déjà une variation d’environ 1,2 dB.
- De plus, en mesure, la norme CISPR 16-4-2 précise que les incertitudes peuvent être importantes.
Exemple : jusqu’à 5,2 dB d’incertitude (facteur ≈ 1,82) pour un test d’émission rayonnée.
Ce qui importe réellement dans ces conversions, ce n’est pas la précision au centième de décibel, mais d’avoir le bon ordre de grandeur rapidement.
Les condensateurs
Article en préparation
Les inductances
Article en préparation